This article gives a sense of how matrix operations such as matrix multiplication arise in machine learning.

Dense layers

Before we get started, there is a small bit of prerequisite knowledge about “dense layers” of neural networks.

1. What is a “dense layer”? Don’t worry about how “dense layers” fit into the big picture of a neural network. All we need to know is that a dense layer can be thought of as a collection of “nodes”.

2. Well now we’ve begged the question: what is a “node”? A node can be thought of as a machine, associated with a set of numbers called weights, that is responsible for producing a numeric output in response to receiving some number of binary (i.e. 0 or 1) inputs. Specifically, if a node N is associated with n weights w₁, …, w_n, then, when n binary numbers x₁, …, x_n are given to N as input, N will compute the following “weighted sum” as output:

For example, if a node has weights 3, 4, 5 and is passed the binary inputs 1, 0, 1, then that node will return the weighted sum 3 * 1 + 4 * 0 + 5 * 1 = 8.

That’s it! We are done with covering prerequisites. We now know what a dense layer of a neural network is responsible for accomplishing: a dense layer contains nodes, which are associated with weights; the nodes use the weights to compute weighted sums when they receive binary inputs.

Matrices

Now, we see what happens when we consider all of the nodes in a dense layer producing their outputs at once.

Suppose L is a dense layer. Then L consists of m nodes, N₁, …, N_m for some whole number m, where the ith node N_i has n weights* associated with it, w_i1, …, w_in. When N_i receives n binary (0 or 1) inputs x₁, …, x_n, it computes

Since the above weighted sum is computed by the ith node, let’s refer to it as f(N_i):

The nodes N₁, …, N_m will need to compute the weighted sums f(N₁), …, f(N_m):

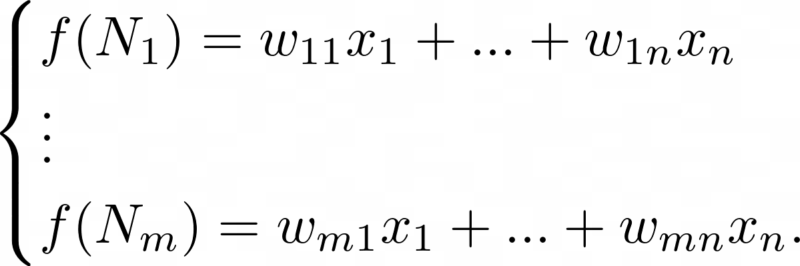
The above can be rewritten with use of so-called column vectors:

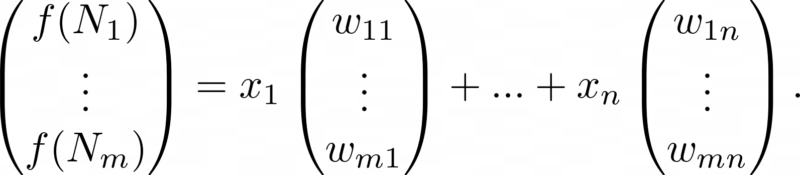
A column vector is simply a list of numbers written out in a column. Note that in the above we have made use of the notions of “column vector addition” and “scaling of a column vector by a number”.

The above expression can be expressed as a matrix-vector product:

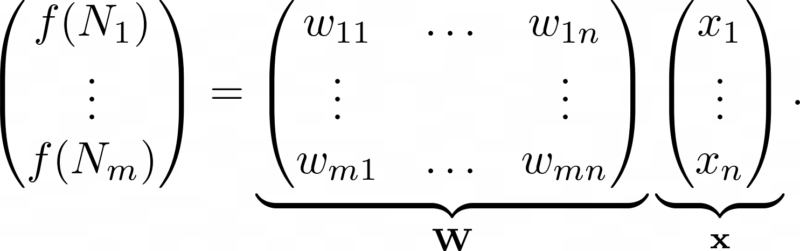
(The matrix-vector product Wx of the above is literally defined to be the expression on the right side of the previous equation).

This matrix-vector product notation gives us a succinct way to determine what each node in a layer does to inputs x₁, …, x_n.

Generalization

The above approach generalizes in the following way. Assume that instead of n inputs x₁, …, x_n, we have p groups of inputs, where the ith group has inputs x_1i, …, x_ni. Additionally, define x_i := (x_1i, …, x_ni) and let f(N_j, x_i) denote the result of node N_j acting on x_1i, …, x_ni. Then we have

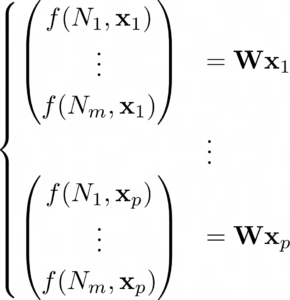
This is equivalent to

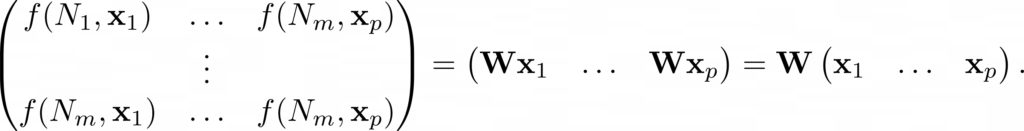
Further generalization

Now, assume that in addition to having multiple groups of inputs x₁, …, x_p, we want to pass these groups of inputs through multiple layers multiple layers L₁, …, L_l. If layer L_i has weight matrix w_i, then the result of passing x₁, …, x_p through L₁, …, L_l is the following product of matrices:

* You may object and remark that the number of weights associated with a given node depends on the node; in other words, that node each node N_i has n_i weights associated with it, not n weights. We are justified in assuming that n_i = n for all i because we can always associate extra weights of 0 to nodes that don’t already have the requisite n weights associated with them.